안녕하세요.
인공지능을 하기 위해서 수학기초가 필요합니다. 그래서 길벗에서 나온 책(모두의 인공지능 기초 수학)을 따라 해보며 확인 겸 정리해 보았습니다.
1. 평균변화율
미분은 변화율을 구하는 것으로 x가 변하는 양에 대해 y가 얼마나 변하는지 구하는 변화율로 평균변화율과 순간변화율이 있습니다.
1) 순간변화율 : 순간의 찰나의 변화에 대한 변화율을 구하는 것을 미분이라고 하고, 그 찰나의 변화율을 순간변화율 혹은 미분 계수라고 합니다.
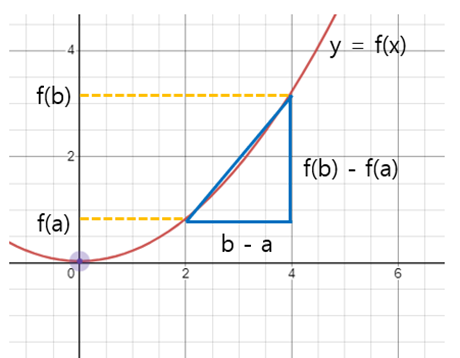
2) 평균변화율 : 함수 y = f(x)가 있을 때 (y의 증가량 = ∆y) / (x의 증가량 = ∆x)을 의미
(예로 x가 2에서 9까지 증가했다면 평균변화율은 ∆x = 9 - 2 = 7 이 됩니다
x가 a에서 b로 변할 때 일반화하면 아래와 같습니다.
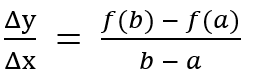
다른 방식으로 △x를 h로 치환하여 표현하여 조금 다르게 표현할 수 있습니다.
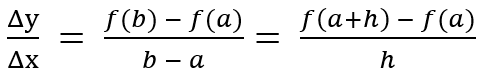
2. 소스 실행하기
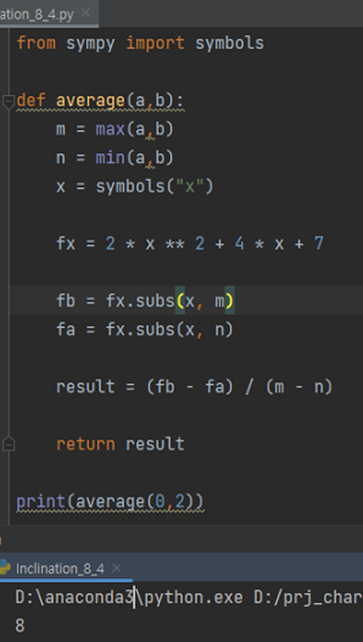
- 책에 나온 소스를 실행해 봅니다. Symbols 라이브러리를 이용해서 x를 기호변수로 바꾸고 fx 함수는
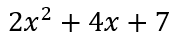
로 정의하고 fx.subs(변수, 대입값) 함수를 이용해서 y값들을 구합니다.
최종적으로 두 점 (0, 4), (2, 12)의 평균변화율을 구하면 8이 나오는 것을 확인할 수 있습니다.
from sympy import symbols
def average(a,b):
m = max(a,b)
n = min(a,b)
x = symbols("x")
fx = 2 * x ** 2 + 4 * x + 7
fb = fx.subs(x, m)
fa = fx.subs(x, n)
result = (fb - fa) / (m - n)
return result
print(average(0,2))
<참고 도서>
1. 모두의 인공지능 기초 수학
반응형
'Programming > Python' 카테고리의 다른 글
| [Python] 필요할 때 찾아보는 연산자(비트연산자, 비교연산자) (0) | 2024.06.12 |
|---|---|
| [Python] 필요할 때 찾아보는 연산자, 복합연산자, 우선순위, 시프트 연산자 (0) | 2024.05.04 |
| [Python] 거듭제곱, 인수분해 구하는 방법 (0) | 2024.03.14 |
| [Python] SymPy 라이브러리를 이용한 방정식 계산방법 (0) | 2024.03.12 |
| [Python] 실제 온도 데이터를 반영한 기간별 온도 가상의 온도 데이터 생성해 보기 (0) | 2024.02.23 |